九宫数独的解法与技巧 数独万能解法数独口诀

九宫数独的解法与技巧：利用数独中行、列和宫内不能填入相同数字的规则，利用已出现的数字对同行、同列和同宫内其他格进行排斥相同数字的方法；当某行中只有一个空格时，由于其他八个数字都出现了，因此这个唯一的空格的数字就确定了。

先认识一下九宫数独，如下图，就是一个空白的九宫数独，分为九行九列九宫，为了方便交流，我们从上到下称为第一行、第二行、第三行、……、第九行，从左到右成为第一列、第二列、第三列、……、地九列，将宫从左到右从上到下依次称为第一宫、第二宫、……、第九宫。

空白的九宫数独

九宫数独的规则和四宫数独、六宫数独的规则相似，在每行每列每宫里只能出现1、2、3、4、5、6、7、8、9这九个数字各一次。

根据规则，我们可以得到一个最简单的九宫数独的解法，唯一数法。

行唯一数法：当某行中只有一个空格时，由于其他八个数字都出现了，因此这个唯一的空格的数字就确定了。如下图：

行唯一数法

第二行中只有第九列一个空格，其他数字出现了5、8、4、1、3、9、2、7，因此空格中只能填6。

行唯一法

列唯一数法：当某列中只有一个空格时，由于其他八个数字都出现了，因此这个唯一的空格的数字就确定了。如下图：

列唯一数法

第六列中只有第六行一个空格，其他数字出现了7、9、1、2、3、8、4、6，因此空格中只能填5。

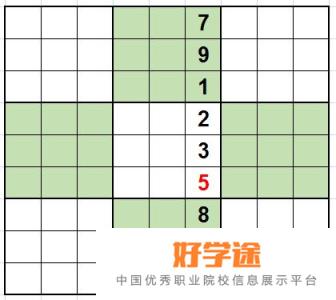
列唯一数法

宫唯一数法：当某宫中只有一个空格时，由于其他八个数字都出现了，因此这个唯一的空格的数字就确定了。如下图：

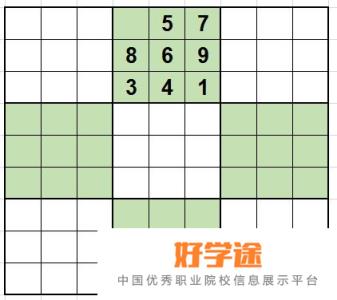
宫唯一数法

第二宫中只有一个空格，其他数字出现了5、7、8、6、9、3、4、1，因此这个空格只能填2。

宫唯一数法

隐性唯一数法：当某行或者某列或者某宫只有两个空格时，可以考虑隐性唯一数法。

行隐性唯一数法：当某行中只有两个空格时，由于其他七个数字都出现了，因此这两个空格的数字就只能是两个数字中的一个，这时去观察和这两个空格相关的列和宫，如果列和宫里有这两个数字中的一个，则可以确定这两个空格中的数字。如下图：

行隐性唯一数法

第四行只有两个空格，其他数字出现了6、7、9、4、3、2、1，因此这两个空格中只能是5和8，看这两个单元格所在的第二列和第四宫，第八列和第六宫，发现第二列有8，因此第四行的第二列就不可能是8，只能是5，第四行的第八列就是8。

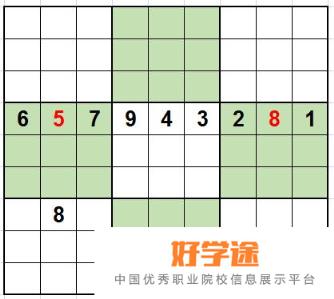
行隐性唯一数法

再看一个例子，如图：

行隐性唯一数法

第六行只有两个空格，其他的数字出现了5、4、8、7、2、6、3，因此这两个空格只能填1和9，再看这两个单元格所在的列（第三列，第9列）和宫（第四宫，第六宫），发现第六宫有1，因此第六行第三列就只能填1，第六行第九列就只能填9。

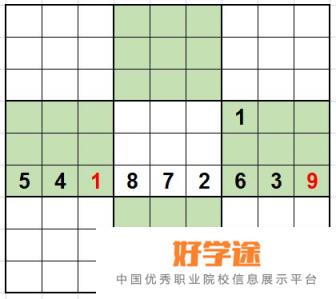
行隐性唯一数法

列隐性唯一数法：当某列中只有两个空格时，由于其他七个数字都出现了，因此这两个空格的数字就只能是两个数字中的一个，这时去观察和这两个空格相关的行和宫，如果行和宫里有这两个数字中的一个，则可以确定这两个空格中的数字。如下图：

列隐性唯一数法

第五列只有两个空格，其他的数字出现了5、4、6、7、9、2、3，因此这两个空格中只能是1和8，再观察和这两个空格相关的行（第六行、第七行）和宫（第五宫、第八宫），发现第六行有1，因此第五列第六行就不可能是1，只能是8，这样第五列第七行就是1。

列隐性唯一数法

再看一个例题，如图：

列隐性唯一数法

第三列只有两个空格，其他数字出现了4、3、6、1、7、9、2，因此这两个空格中只能填5和8，再看这两个空格所在的行（第六行、第九行）和宫（第四宫、第七宫），发现第四宫有8，因此第三列第六行就不可能是8，只能是5，第三列第九行就是8。

列隐性唯一数法

宫隐性唯一数法：当某宫中只有两个空格时，由于其他七个数字都出现了，因此这两个空格的数字就只能是两个数字中的一个，这时去观察和这两个空格相关的行和列，如果行和列里有这两个数字中的一个，则可以确定这两个空格中的数字。如下图：

宫隐性唯一数法

第五宫只有两个空格，其他的数字出现了3、7、5、2、8、9、6，因此这两个空格只能是1和4，再观察这两个空格所在的行（第四行、第六行）和列（第六列），发现第四行有1，因此第五宫的第四行第六列就不可能是1，只能是4，第六行第六列就是1。

宫隐性唯一数法

利用这两个方法，试试看完成下面的题目吧